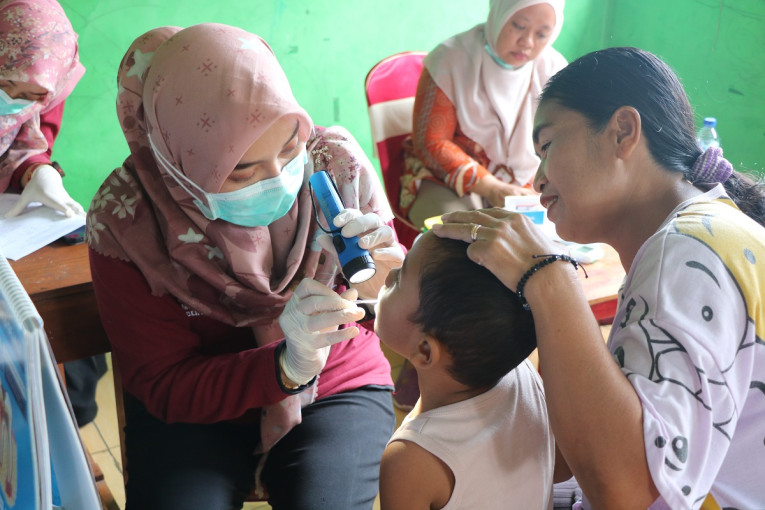
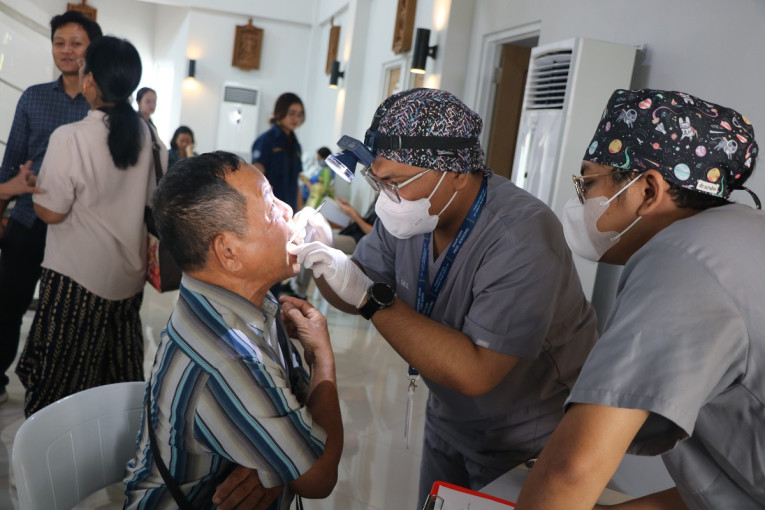
UGM Gelar Pemeriksaan Kesehatan Gratis di Desa Getas
Sebanyak 300 warga Desa Getas, Kecamatan Kradenan, Kabupaten Blora, Jawa Tengah mengikuti kegiatan pemeriksaan kesehatan gratis yang diselenggarakan Universitas Gadjah Mada bersama Pertamina...